• 著者略歴等	1979年日本通運株式会社入社。1997年より日通総合研究所で、メーカー、卸の物流効率化、コスト削減などのコンサルティングと、国土交通省や物流事業者、荷主向けの研修・セミナーに携わる。2014年6月山田経営コンサルティング事務所を設立。 著書に「すらすら物流管理（中央経済社）」「物流コスト削減の実務（中央経済社）」「物流戦略策定のシナリオ（かんき出版）」などがある。中小企業診断士。 URL：http://www.yamada-consul.com/

目次

• Ⅰ．季節変動を加味した需要予測モデル
• Ⅱ．変形指数平滑モデル

Ⅰ．季節変動を加味した需要予測モデル

  前回、もっともシンプルな需要予測の方法として、「単純移動平均モデル」を紹介した。計算がシンプルで使いやすく、予測対象が直近の出荷トレンドに大きく影響を受けるような特徴を持つ商品については、相当程度の予測精度が期待できる。反面、直近のトレンドしか反映しないため、季節や月単位で需要が変動する商品について、変わり目をまたいで予測する場合などには不向きである。
  直近の出荷トレンドと季節変動の両要素を反映できる代表的な予測モデルは、「指数平滑モデル」「ウィンターズ・モデル」の２つである。どちらも過去の出荷データのみを活用して予測を行う点で共通しており、EXCELを使って比較的簡単に予測ができるという意味では実務者向きといえる。需要予測の入門書などでは必ずといってよいほど紹介されている定番である。
  ただ、こうした手法の多くは一般的な計算ロジックや考え方だけが紹介されているだけで、実務で使ってみると、些細なところでつまずいてしまって実用化できないことが往々にしてある。実務では全体概要や理論にくわえ、この「ほんの些細な部分」が大切なことは理解いただけると思う。「神は細部に宿る」のである。
  本稿では指数平滑モデルを対象に、手法のロジックにとどまらず、こうした実務上の重要ポイントまで踏み込んで解説していく。

Ⅱ．変形指数平滑モデル

１．“正統”指数平滑モデル

  正確にいえば、指数平滑モデルによる予測には季節変動は加味されない。そこで筆者が季節変動を反映するように（勝手に）アレンジした「変形指数平滑モデル」を紹介するのだが、まずはその前に「正統」モデルを解説しておく。予測値は以下の式で求める。

  月単位で予測しているが、もちろん期、日などに置き換えてもかまわない。この式でαはパラメータと呼ばれ、0～1の間の値をとる。前月の予測値とは、前々月に予測した前月予測値である。少々ややこしい言い方になるが、αの値が0.5であれば、当月の予測値は直近である前月の実績と前々月時点での前月予測値を半分ずつ反映したものになる。αが1に近づくにしたがって、前月実績の重みが増すので、直近実績重視となる。逆に前月予測値の重みが増せば、より古いデータの重みが増していく。つまり指数平滑モデルは新しいデータを重視するか、古いデータを重視するかといった判断基準で予測を行う。
  ある程度トレンドを（遅れて）反映させることはできるが、季節変動を加味するのは難しい。とくに季節の変わり目で需要が大きく変動する場合などにはほとんど役に立たない。

２．変形指数平滑モデル

  実際、多くの商品に季節変動や特定の月に需要が集中する傾向があるので、指数平滑モデルを実務で使うのには無理があることが多いように思う。
  そこで季節変動を反映させるよう筆者なりに変形した指数平滑モデルの算出式が下記である。

  このモデルでは、前月実績にパラメータαを乗じた値に、前年同月実績に（１－α）を乗じた値を合算する。αが0.5より大きければ直近の需要動向を、0.5より小さければ前年同月をそれぞれ重視した予測値になる。前年同月の需要は季節変動が反映されているものと考えれば、この式は直近のトレンドと季節変動の２つの要素を加味したものといえる。
  ここまでは単純な理屈であるが、問題は0から1までのあるパラメータαの値をどう決めるかということである。ここが実務上もっとも悩む点であり、指数平滑法のキーポイントである。
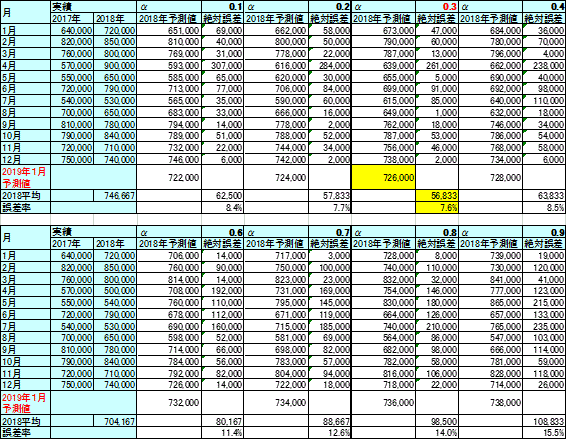
  最適なパラメータを決めるには、「過去の実績で（答えの出ている）過去を予測」してもっとも予測誤差が少ない値を探すのが有効である。図表1を参照願いたい。この表では、2017年と2018年の月別出荷実績が把握されている。このデータをもとに変形指数平滑法により2019年1月の出荷予測を行ってみよう。最適なパラメータαを求めるため、過去のデータで過去の実績を予測してみる。具体的な手順は以下のとおりである。

図表1　変形指数平滑法による予測

  ここでは2017年の実績をもとに、0.1から0.9までのαを使って（すでに答えの出ている）2018年の予測を行う。最適なαを求めるための試行錯誤を行うわけである。2018年の実績はすでに確定しているので、この方法によりそれぞれのαに対応した予測値と実績の差が求められる。
  たとえばα=0.1の場合の2018年1月の予測値は「2017年12月（前月）実績“750,000”×0.1＋2017年1月（前年同月）実績“640,000”×（1-0.1）＝651,000」となる。この予測値と2018年1月実績の誤差は69,000となる。この予測を2018年1月から12月まで行い、誤差の月平均を求める。これをα0.1から0.9まですべて行うわけである。なお、誤差には絶対誤差という値を使う。絶対誤差とは差異をすべてプラスに換算したものである。通常、誤差はプラスになったりマイナスになったりするが、これを単純に合計してしまうとプラスとマイナスが相殺されて、誤差の絶対的な大きさがわからなくなってしまうからである。
  こうして算出した各絶対誤差の月平均と2018年実績の月平均を比較して誤差率を求める。誤差率が最も小さいパラメータαが最適なパラメータということになる。表ではα＝0.3のとき、絶対誤差の平均が56,833、誤差率7.6％で最小、つまり最適なパラメータとなった。このα＝0.3を先の算出式に入れて2019年1月の予測を行えば、おおよそ7％内外の誤差率で的中するはず、と仮定するわけである。
  2019年1月の予測は、先のモデルにしたがって「2018年12月（前月）実績“740,000”×0.3＋2018年1月（前年同月）実績“720,000”×（1-0.3）＝726,000」となる。
  直近の実績に0.3、前同に0.7を乗じたことにより、直近のトレンドよりいくぶん、季節（月別）波動を重視した予測という結果になった。
  変形指数平滑モデルは理屈も計算方法が単純でわかりやすく、使い勝手がいい。

３．ソルバーでパラメータを求める

  ただし、ここで問題となるのがやはりαの求め方である。EXCELを使えば手間がかからないとはいえ、0.1から0.9まで試行錯誤するのはあまりスマートとはいえない。それ以前に、実際のパラメータは端数を含めた0から1の間をとるのであって、切りのよい数字になると仮定するのには無理がある。
  こうした面倒な手作業を繰り返さなくてもEXCELには便利な機能がある。それが「ソルバー」である。ソルバーは条件さえ指定すればその中で最適な答えを瞬時に導き出してくれる大変心強い機能である。
  少々細かくなるが、今回の事例にしたがって手順を説明する。
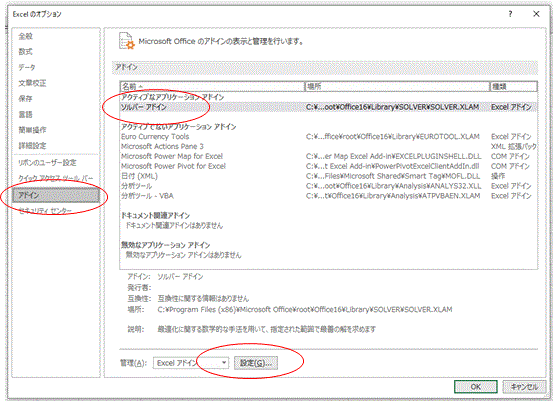
  通常、ソルバー機能はEXCELに備わっているのだが、まずは「アドイン」して機能を有効化する必要がある。
①EXCELの「オプション」の中から、「アドイン－ソルバーアドイン－設定」の順にクリックする。これでソルバー機能が有効化される（図表2）。

図表2　ソルバーアドイン

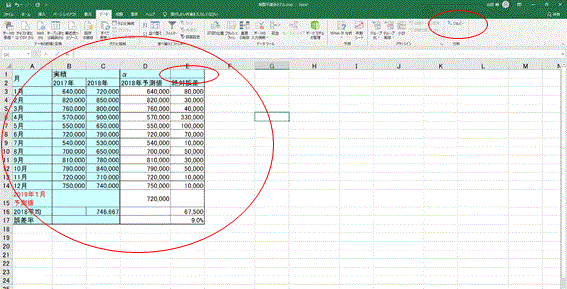
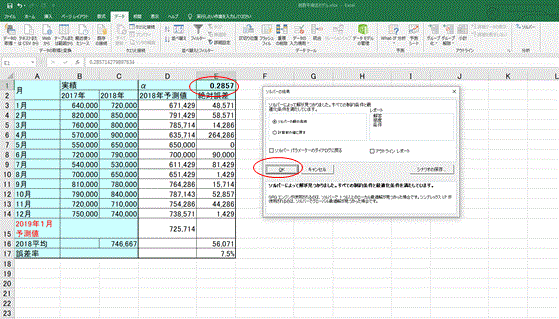
②先の2017年、2018年の実績と予測を求める式を挿入した表を作成し、データメニューの「ソルバー」をクリックする（図表3）。αの値はE1のセルとなるがこの段階では何も入れないでおく。予測値はαがゼロで計算されるので、この時点ではすべて前年同月実績となる。

図表3　予測式作成とソルバー機能を指定

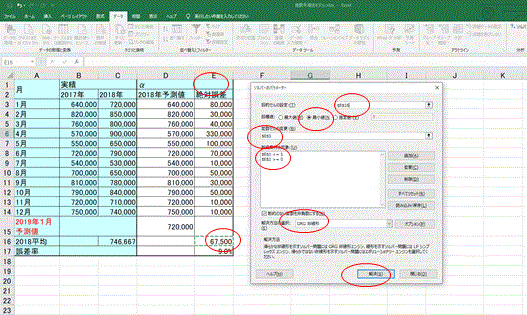
③「ソルバーのパラメータ」で条件を指定する。目的のセルは絶対誤差の平均「$E$16」、目標値は「最小値」、変数セルはパラメータα「$E$1」、制約条件の対象「$E$1<＝1、$E$1>＝0」、解決方法の選択は「GRG非線形」と指定し、「解決」をクリックする（図表4）。

図表4　ソルバー条件の指定

④ソルバーが実行され、指定した条件での最適なパラメータ「0.2857」（便宜的に小数点以下4桁まで表示）の値が示される。

図表 5　ソルバー実行の結果

  手作業による試算では0.3であったパラメータがソルバーにより0.2857と、より正確な値となった。その結果、誤差率は7.6％から7.5％に縮小し、予測値は726,000から725,714と精緻化された。
  変形指数平滑モデルは、ソルバー機能を利用することによって、より簡易により正確に算出できる。
  今回は紙面の都合もあり、ウィンターズ・モデルを紹介できなかった。ただ、ウィンターズ・モデルは計算が非常に複雑になりため、EXCELで実行するには少々無理がある。それでいて、筆者が両モデルを実際に運用した経験では変形指数平滑モデルの方が誤差は少ないという結果も出ている。実務上では使い勝手のよい変形指数平滑モデルで十分と思われる。
  海外生産品の在庫管理を行う上で、ポイントとなる簡易的な需要予測の方法を紹介してきた。今回はいくぶんテクニカルな内容となってしまったが、確立されたロジックに基づいて需要予測を行い、実績との乖離を検証してみる意義は決して小さくないと考える。需要予測に関心のある方はぜひ一度試してみてはいかがであろうか。

以上