略歴	1948年 1974年岡山県生まれ。 1997年神戸商船大学卒業。 2008年神戸大学大学院修了、博士（工学）。 広島商船高等専門学校、 流通科学大学商学部教授を経て、2025年より現職。 主な著書に、『物流のしくみ』（単著、同文舘出版、2023年）、『モーダルシフトと内航海運』（共著、海文堂出版、2020年）、『1からの流通論 第2版』（共著、碩学舎、2018年）がある。

目次

• １．はじめに
• ２．物流とOR
• ３．物流施設の最適配置
• ４．ソルバーの能力向上がもたらした成果
• あとがき

  

１．はじめに

正直、何をネタにして書こうか迷った。決してネタが豊富で選別に困ったという話ではない。前職、流通科学大学時代の物流企業と学生の社会連携（コラボ）は、第562号（髙橋先生、近畿大学の事例）と重なる点が多いし、最近始めたフィジカルインターネットの研究は、まだ理解に乏しい。そこで、ずいぶん昔に取り組んだ研究ネタではあるが、物流施設の配置問題、特にその解法を中心に話をしてみたい。ざっとではあるが、『ロジスティクス・レビュー』のバックナンバーのタイトルを確認したところ、物流センターや倉庫などの物流施設の配置問題を取り上げた事例は思ったより少なく、特にOR（Operations Research）を用いて物流施設の最適配置を求めるといった類の内容は確認できなかった。ただ単に、ニーズが少ないだけかも知れないが、話題が重ならないという点を拠り所としたい。
もう20年前になるが、当時、大手宅配事業者の物流ネットワークの効率性を検証したことがある1)。今も大きな違いはないと思うが、これらの宅配事業者は、地域間輸送の中継となる主管支店などのセンター（上位拠点）と地域内の集配送を担う営業所などのデポ（下位拠点）を機能別に分け、それらを階層的に配置し、下位拠点で集められた宅配貨物を上位拠点に集約し、上位拠点間にて幹線輸送が行われていた。研究では、宅配貨物の発生集中量は人口分布との相関があることから、町丁目単位の人口を基に、下位拠点の最適配置を求めたうえで、下位拠点からみた上位拠点の最適配置を求めることにより、物流ネットワークの効率性を検証したわけである。問題を解くにあたっては、OR分野における最適配置問題の一つであるp-median問題を適用した。しかしながら、当時のソルバーエンジンの計算能力とPC環境では、大きな規模の問題を解くことが出来ないという課題にも直面した。
それから20年、当然ではあるが技術の進歩は目覚ましい。PCの性能もさることながら、ソルバーエンジンの計算能力が飛躍的に向上している。これは、高機能なソルバーエンジンであるGurobi2)を無料で経験した実感である。ありがたいことに、教育機関であれば、無料もしくはアカデミックプライスで使用可能であることが多い。単に、物流施設の配置問題の解法を取り上げるだけではもったいないので、こうした技術革新にも触れたい。

２．物流とOR

よく言われるように物流とORの親和性は高い。というよりも、物流に関する定量的な問題を解く際は、数理的なアプローチ、すなわちORの援用は欠かせないと考える。
物流分野における典型的なORの応用事例を挙げてみたい。1つ目は、トラックが複数の配送先に効率よく商品を届けるルートを最適化する“輸配送計画”である。VRP（Vehicle Routing Problem）が代表的である。2つ目は、需要予測に基づき発注量・在庫水準を決定する“在庫管理”である。経済発注量（EOQ）や安全在庫を求めることが多い。3つ目は、どこに物流センターや倉庫を設置すれば、総コストが最小になるかを決定する“施設配置問題”である。weber問題やp-median問題として定式化し、解かれる。
公益社団法人日本オペレーションズ・リサーチ学会が提供しているOR辞典によると、「ORとは、現象を抽象化した数理モデルを構築し、モデル分析に基づいて種々の問題、とりわけ意思決定問題の解決を支援する方法論や技法の総称」とある。先の事例でも示したように、物流分野における現象をモデル化（定式化）し、実際の現場で得られる膨大なデータをもとに、コスト最小化や効率性の最大化を目的関数として、輸配送計画、在庫管理、物流施設の最適配置、などにて最適解を導出するためにORが用いられる。
同学会の機関誌『OR』の全文検索(注1)にて、“輸配送計画”、“在庫管理”、“物流施設”のキーワードを検索すると、順に388件、233件、61件と多くの論文がヒットする。なお、いまから約70年前の記念すべき最初の機関誌Vol.1（1956年）では、挨拶に続いて、トップバッターとして「適正在庫及び在庫管理の問題（横山保、大阪大学経済学部）」が掲載されている。さらに、同号では実務家からも「輸送計画の一例（岡見賢一、武田薬品工業（株））」が報告されていることから、ORの学問領域の初期の頃からすでに物流分野への応用が試みられていることが伺える。

３．物流施設の最適配置

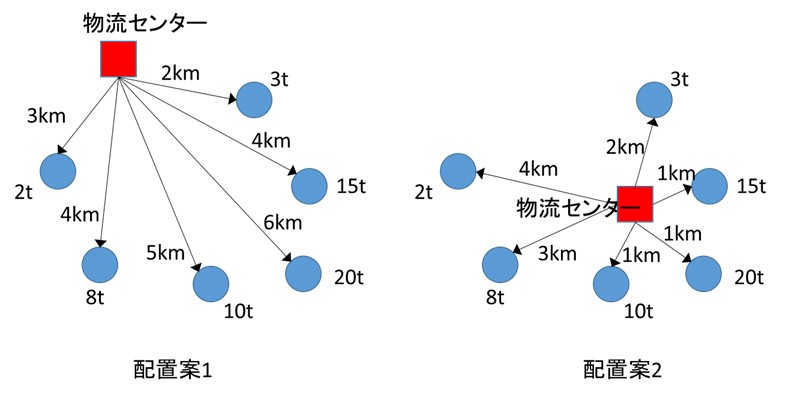
物流施設である物流センターの立地は、用地の広さや地価の安さ、高速道路ICへのアクセス性、さらには需要地への近接性なども考慮する必要があるが、ここでは、単純化するため、図1に示すような配送先（図中の丸印）との位置関係のみで考える。配置案1と2のケースでは、どちらが最適な配置であるかは一目瞭然である。トンキロを使って定量的に比較すると、配置案1が274トンキロであるのに対し、配置案2では83トンキロと3分の1以下となっている。つまり、配送先との関係のみで物流施設の最適配置を求めるというのは、輸送コストである配送量（需要量）×距離の総計が最小となるような物流施設の配置を求めることである。これは、配送量（需要量）をQ、距離をDとおくと、式(1)のように定式化することができる。なお、距離については、道路距離の方が好ましいが、計算が煩雑になるため、直線距離（ユークリッド距離）を用いる。

Minimize ΣQ*D 式(1)

図1　配送先からみた物流センターの配置案の比較
*画像をClickすると拡大画像が見られます。

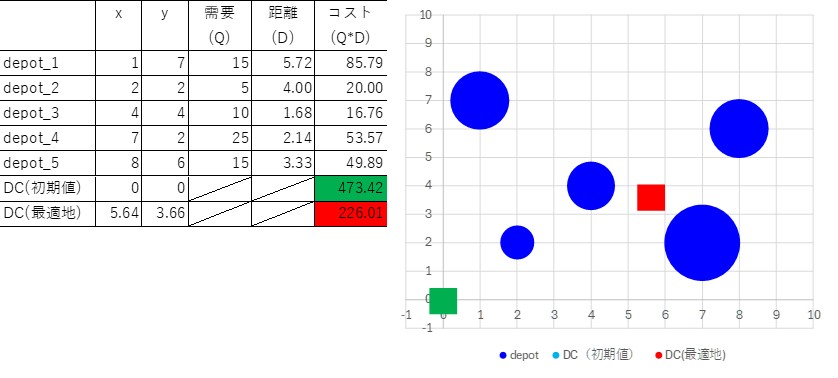
定式化ができれば、プログラムや汎用ソルバーを用いて、計算問題を解く。Microsoft Excelにもソルバー機能は備わっており、図2のような問題であれば簡単に最適配置を求めることができる。配送先はdepot_1～5の5か所であり、それぞれ需要量（Q）がある。散布図では、depotの位置と需要量の大きさを円で示している。物流センターDCと各配送先の距離（D）はユークリッド距離により算出し、Q*Dによりコストを求める。まず、初期値としてDCのx,y座標を（0,0）としておく（散布図の緑の四角）、このときのQ*Dの合計である総コストは、緑のセルの473.42である。ソルバー機能を使って、計算する際は、赤のセルの総コストが最小になるように、DC（最適地）のx,y座標を変化させる。その結果、座標（5.64, 3.66）の位置（散布図の赤い四角）が物流センターの最適配置であり、総コストは226.01である。
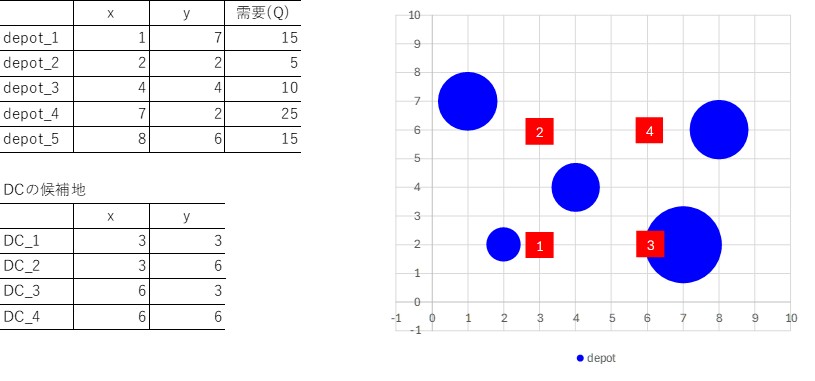
以上のようにして、最適配置が求まったわけであるが、物流センターは2次元の座標平面上であれば、どの場所にでも自由に配置できる。つまり、x,y座標のどのような値（連続量）をとることもできる。こうした連続量を扱う配置問題をweber問題という。しかしながら、何処にでも自由に施設を配置するというのは非現実的であり、物流センターなどの施設の配置を検討する際は、候補地から選定するケースが多い。このような問題に対応するため、複数の候補地の中からp箇所を選ぶ配置問題のことをp-median問題という。図3に示すように、配送先であるdepotの条件は先ほどと同様であるが、物流センターDCの候補地が4か所（DC_1～4）与えられ、その中から最適な配置を選択する。1か所（p=1）のみ選択する場合、図2の結果に近いDC_3が良さそうである。2か所（p=2）であれば、どうであろうか。1つ目はDC_3、2つ目はDC_3から離れているdepot_1をカバーするために、DC_2が選ばれそうである。実際にExcel以外のソルバーで計算した結果(注2)、p=2の場合であれば、DC_2とDC_3が選択され、総コストは165.96であった。
一見すると、p-median問題も容易に最適解が得られるように思えるが、weber問題が連続量を扱う問題であるに対し、p-median問題は候補の中から選択する（選択:1、非選択:0）


図2　weber問題による物流センターの配置案の検討
*画像をClickすると拡大画像が見られます。

図3　p-median問題による物流センターの配置案の検討
*画像をClickすると拡大画像が見られます。

離散問題である。離散問題は組み合わせ問題であり、計算量（組み合わせの数）が膨大になり、PCの性能が向上したとしても解くことが難しいことで知られている。

４．ソルバーの能力向上がもたらした成果

式(2)が、宅配事業者の物流ネットワークの効率性を検証するために定式化したp-median問題である。今までの説明と同様に、Qは需要量（宅配貨物量）、Dは直線距離であり、これらは連続量であるものの、yjとxijが{0,1}の離散量となっている。yjは、上位拠点を候補地jに立地させる否かを示す変数であり、xijは、下位拠点iが上位拠点jに属するか否かの変数である。こうした連続量と離散量の両方が含まれる問題を、混合整数線形計画問題（MILP:Mixed Integer Linear Programming）と呼ぶが、離散量である整数が含まれることから、先に述べた通り、計算の難易度は高い。このため、当初、近畿2府4県を対象に物流ネットワークの効率性を検証しようとしたが、断念し、兵庫県のみに限定したという経緯がある。ただし、これは論文の信憑性を脅かすものではない。


式(2)
*画像をClickすると拡大画像が見られます。

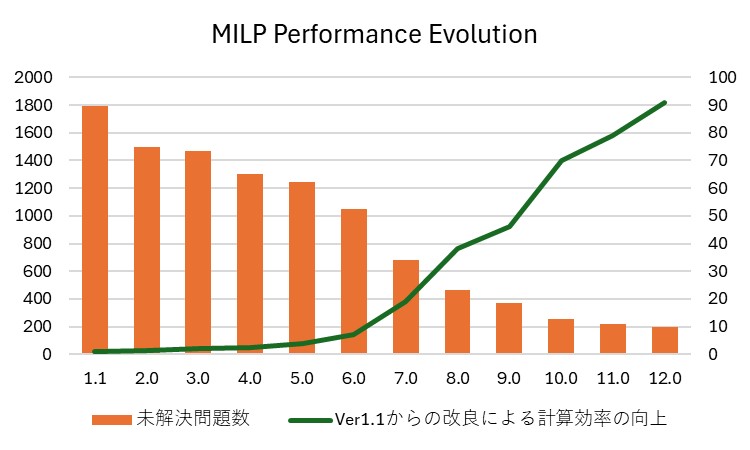
近畿圏の検証結果に入る前に、今回解析に使用したソルバーエンジンであるGurobi Optimizerの能力向上に触れたい。Gurobiは 2008年に、Robert Bixby氏、Edward Rothberg氏、Zonghao Gu氏、の3氏によって開発される。図4は、MILPを対象としたベンチマークテストの結果である。最初のリリースのバージョン1.1では解けない問題が1,800あったのに対し、改良を重ねた結果、2024年11月にリリースされた最新のバージョン12.0では、未解決問題が200まで、大幅に減少している。同様に計算スピード（図中の第2軸）も初期バージョンに比べて、最新バージョンでは91%と大幅に向上している。このように、Gurobi Optimizerはソルバーエンジンとしての能力向上が著しい。


Gurobi社のホームページを参考に筆者作成
図4　ソルバーエンジン（Gurobi Optimizer）の能力向上
*画像をClickすると拡大画像が見られます。

分析結果の詳述は避けるが、Gurobiをソルバーエンジンとすることにより、近畿圏（2府4県）の宅配網の物流ネットワークの効率性を検証することが可能となった。もちろん、PCスペックの向上による影響も無視できないと思うが、普段使っているPC（CPU：Intel 3.10GHz、RAM：16.0GB）は、それほど高性能というわけでもない。なお、20年前のPCのスペックは、CPU：Intel 2.26GHz、RAM：1.0GBである。専門家ではないので、PCの性能向上なのか、ソルバーエンジンの能力向上なのか、どちらが問題を解くのに強く影響したかを見極めることはできないし、その点に強い関心があるわけでもない。それよりも20年前に解けなかった問題が、わずか1秒もかからず（0.64s）解けたことに感動した。

あとがき

Gurobiは、ソルバーのため、実際の問題（p-median）を解くためには、プログラムを組む必要がある。達人たちのホームページを拝見すると、言語にPythonを使っているケースが大半だったことから、新しい言語にチャレンジした。プログラム言語を触るのも久しぶりなため（前々職の高専時代以来）、相当苦戦した。というより、途中から自分では組める気がしなかったので、ダメもとでChatGPTにお願いしてみた。普段、あまりChatGPTを使うことが無かったので、半信半疑だったが、何回かのやり取りで、こちらが希望する通りのプログラムを組んでくれた。コードも簡潔で分かりやすく、これには驚かされた（もう、プログラムを習得する必要がないじゃないかと）。このあたりの苦労話（？）も機会があれば、してみたい。また、近畿圏の分析結果は、フィジカルインターネットセンターとの共同研究のため、承諾が得られれば、こちらも話題提供したい。


【補注】
(1)2006年以降（1990年-2005年は特集タイトルのみ）の機関誌記事全文検索
(2)事例で取り上げた簡易な問題であれば、Excelでも算出可能であるが、計算手順が煩雑になり、一般的ではないため、汎用ソルバーにて計算。
【参考文献・URL】
1)田中康仁, 小谷通泰，「宅配貨物輸送における配送拠点の最適配置計画に関する分析」，土木計画学研究・論文集，Vol.23，no.3，pp.779-787，2006年
2)https://www.gurobi.com/　（2025/09/03閲覧）


(C)2025 Yasuhito Tanaka & Sakata Warehouse, Inc.